Soluções Astronomia - Semana 17

Iniciante

Como o eixo maior do cruzeiro do Sul tem $6^{\circ}$, podemos dizer que a distância de $\alpha Cru$ até o PCS, pelo método que o nosso hemisfério usa será:

$d=4.5*6=27^{\circ}$

Com isso, a declinação de $\gamma Cru$ será:

$\left | \delta_{\gamma} \right | =90-(27+6)=57^{\circ}$

Intermediário

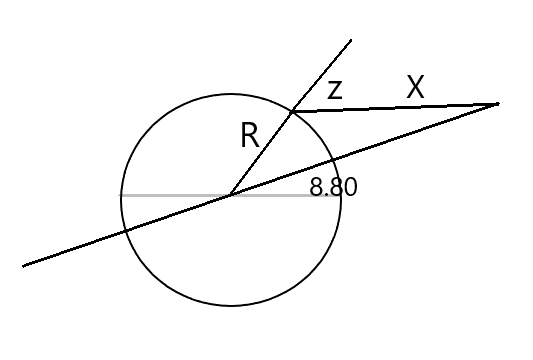
Com base na construção acima,e colocando a distância do satélite em função do raio da terra, podemos escrever, por lei dos cossenos:

$x^{2} =R^{2} +(36.72R)^{2} -2*R*36.72R*cos(34.9)$

$x=35.9R$

Com isso, por lei dos senos

$\frac{sen(180-z)}{36.72R} =\frac{sen(34.9)}{35.9R}$

$z=35.81^{\circ}$

Avançado

Escrevendo a equação de magnitudes para a configuração normal e primeiro eclipse:

$m_{s} -m_{p} =-2.5log\frac{R_{1}^{2} T_{1}^{4} + R_{2}^{2} T_{2}^{4}}{R_{1}^{2} T_{1}^{4}}$

$\Rightarrow \frac{ R_{2}^{2} T_{2}^{4}}{ R_{1}^{2} T_{1}^{4}} =2.177$

Escrevendo novamente para a configuração normal e o segundo eclipse:

$m_{s} -m_{s2} =-2.5log\frac{R_{1}^{2} T_{1}^{4} + R_{2}^{2} T_{2}^{4}}{R_{2}^{2} T_{2}^{4} +(R_{1}^{2} -R_{2}^{2})T_{1}^{4}}$

$m_{s} -m_{s2} =2.5log(1-\frac{R_{2}^{2} T_{1}^{4}}{R_{2}^{2} T_{2}^{4}(\frac{R_{1}^{2} T_{1}^{4}}{R_{2}^{2} T_{2}^{4}} +1)})$

$\Rightarrow \frac{T_{1}}{T_{2}} =1.041$