Escrito por Sofhia Souza
O uso da linguagem dos conjuntos nos permite resolver diversos tipos de problemas. O Princípio da Inclusão e Exclusão (PIE) é o que iremos trabalhar nesta aula, e para ilustrarmos a maneira que iremos aplicá-lo, usaremos do seguinte problema: contar quantos são os números entre 1 e 1000 que são divisíveis por 5 ou por 7.
Chamemos de $$A$$ o conjunto com os múltiplos de 5 e de $$B$$ o conjunto com os múltiplos de 7. Não é difícil determinar $$|A|$$ e $$|B|$$ (usaremos a notação $$|A|$$ para indicar o número de elementos do conjunto $$A$$). A solução do nosso problema é a contagem dos elementos que estejam em $$A$$ ou estejam em $$B$$. Em símbolos, queremos $$|A\cup B|$$. Não podemos simplesmente somar $$|A|+|B|$$, pois alguns elementos serão somados duas vezes, a saber, aqueles que são múltiplos comuns de 5 e de 7, ou melhor, os elementos de $$A\cap B$$ ( o conjunto dos inteiros entre 1 e 1000 que são divisíveis por 7×5 = 35). Assim, temos que a solução do problema é dada por:
$$|A\cup B|=|A|+|B|-|A\cap B|$$
A fórmula acima é a versão mais simples do problema que vamos tratar nesta aula e recebe o nome de Princípio da Inclusão e Exclusão.
Cardinalidade da união de dois conjuntos
Dados dois conjuntos $$A$$ e $$B$$, sendo ambos subconjunto de um conjunto $$S$$, onde $$A\cap B= \varnothing$$. Neste caso é fácil ver que $$|A\cup B|=|A|+|B|$$. O mesmo não se verifica quando $$A\cap B \ne \varnothing$$. De fato, quando $$A\cap B \neq \varnothing$$, os elementos que são comuns, são contados duas vezes. Assim, dados $$A$$ e $$B$$, subconjuntos de $$S$$, o número de elementos de $$A\cup B$$ é dado por:
$$|A\cup B|=|A|+|B|-|A\cap B|$$
Na imagem abaixo é possível visualizar com mais clareza, sendo $$|A| = X+Y$$, $$|B| = Z+Y$$ e $$|A\cap B| = Y$$
Cardinalidade da união de três conjuntos
Sejam os conjuntos $$A$$, $$B$$ e $$C$$, subconjuntos de um conjunto $$S$$. A cardinalidade da união de três conjuntos é:
$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$$
Pois:
$$|A\cup B\cup C| =$$
$$|(A\cup B)\cup C|=$$
$$|A\cup B|+|C|-|(A\cup B)\cap C|=$$
$$|A|+|B|-|A\cap B|+|C-|(A\cap C)\cup (B\cap C)|=$$
$$|A|+|B|-|A\cap B|+|C|-|A\cap C|-|B\cap C|+|A\cap C\cap B\cap C|=$$
$$|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$$
Princípio da Inclusão e Exclusão
Generalizando, é possível dizermos que, dados $$N$$ conjuntos, a união de todos eles é referente a soma de todas as possíveis interseções entre um número ímpar de conjuntos, menos a soma de todas as possíveis interseções entre um número par de conjuntos. Exemplificando:
União de 4 conjuntos $$A$$, $$B$$, $$C$$ e $$D$$ é dada por:
$$|A\cup B\cup C\cup D|=|A|+|B|+|C|+|D|-|A\cap B|-|A\cap C|-|A\cap D|-|B\cap C|-|B\cap D|-|C\cap D|+|A\cap B\cap C|+|A\cap B\cap D|+|A\cap C\cap D|+|B\cap C\cap D|-$$
$$|A\cap B\cap C\cap D|$$
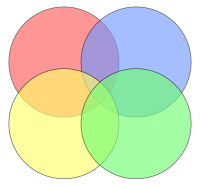
As interseções entre um número ímpar de conjuntos ($$|A|, |B|, |C|, |D|, |A\cap B\cap C|,|A\cap B\cap D|, |A\cap C\cap D|, |B\cap C\cap D|$$) foram somadas, e as interseções entre um número par de conjuntos ($$|A\cap B|, |A\cap C|, |A\cap D|, |B\cap C|, |B\cap D|, |C\cap D|, |A\cap B\cap C\cap D|$$) foram subtraídas.
Exemplo de código
Código do problema Quase Primo, da OBI: