Nível 3 - Fase 3

Soluções de Felipe Martins e Victor Ivo

Para ter acesso à prova teórica da terceira fase da OBF nível 3, clique aqui.

Problema 1:

Esse é um problema bem interessante, pois envolve o conceito de gravidade aparente e de empuxo, nós temos genericamente, que uma partícula livre tende a seguir a direção da gravidade aparente. Contudo, ao colocarmos a partícula num líquido, a mesma deixa de ser livre, pois existirá uma força de empuxo atuando sobre a mesma. O grande segredo é saber que o empuxo sempre atua na direção da gravidade aparente,e contrária a ela, assim temos que:

$\vec{E}=-\rho V \vec{g}$

$\vec{F_{res}}=m\vec{g}+\vec{E}$

E agora,para facilitar a análise da física do problema, escrevamos a força resultante como se fosse um "peso equivalente", que usaremos como artifício para estudar a dinâmica das bolas.

$\vec{F_{res}}=m\vec{g'}=m\vec{g}-\rho V \vec{g}$

$\vec{g'}=\vec{g}(1-\frac{\rho V}{m})$

$m=\rho_{corpo}V=\rho_{c}V$

$\vec{g'}=\vec{g}(1-\frac{\rho}{\rho_{c}})$

Perceba que para uma densidade do líquido maior que a densidade do corpo, teremos uma subtração que resultará num número negativo, o que significa que a "gravidade efetiva" no corpo o levará à direção contrária da gravidade aparente. Vemos que na ausência de rotação a gravidade aparente para as bolinhas aponta para baixo, pois é a própria gravidade gerada pela terra, e com isso a bolinha mais densa segue a direção dela (para baixo) e vai pro fundo do cilindro, a bolinha menos densa vai no sentido contrária da gravidade, pois sua densidade é menor que a da água, assim ela vai pra o mais alto possível no cilindro. Já no caso de uma rotação suficientemente alta dos cilindros, a gravidade aparente será basicamente a aceleração centrífuga, que apontará para fora do centro, a bolinha mais densa segue sua direção, "pra fora", e vai pra o mais longe possível do eixo, alcançando a parte mais extrema, e a mais leve terá uma "gravidade efetiva" pra dentro, o que a fará ficar no fundo do cilindro, que é a parte mais próxima ao eixo. OBS: Não confunda gravidade aparente com o conceito de gravidade efetiva que acabamos de criar para resolver esse problema,a gravidade efetiva foi um artifício usado apena para mensurar o quão maior que o empuxo é o peso aparente,mais você pode trocar qualquer citação de gravidade aparente por uma comparação rápida entre o empuxo e o peso.

Problema 2

Este é um problema de óptica geométrica com uma física não muito complicada, mas que exige certa criatividade do aluno e conhecimento de simetrias, o que é necessário a qualquer bom físico. Usando lei de Snell na face de contato,ou seja, no ponto $P_{1}$ vemos, prolongando a normal,que o ângulo de incidência do raio de luz é $45$ graus.Ou seja:

$n_{1} sen(\theta_{1})=n_{2} sen(\theta_{2})$

$n_{1}=1$ e $n_{2}=\sqrt{2}$

$1 \cdot \frac{\sqrt{2}}{2}=\sqrt{2} sen(\theta)$

$sen(\theta)=\frac{1}{2} \Rightarrow \theta=30^{\circ}$

Assim, o raio de luz sai fazendo um ângulo de $30$ com a normal, e segue uma linha reta até que atinja novamente o cilindro,num ponto $P_{2}$ , do ponto de contato trace uma normal, o triângulo $P_{1}OP_{2}$ , sendo $O$ o centro da circunferência tem dois lados iguais, pois os dois valem R, assim temos um triângulo isósceles e consequentemente o arco de 30 graus aparece também entre a normal à superfície do ponto $P_{2}$ e o raio de luz, e pela reversibilidade ele sai fazendo um ângulo de $45$ graus com a normal. Perceba que o prolongamento da normal é a reta que contém $OP_{2}$ , essa que faz 15 graus com a horizontal, direção original da luz. Assim, nosso novo raio de luz faz um ângulo de $30$ graus com a horizontal (ou - $30$ ,caso você olhe pela direção dele, que é descendo). Nós acabamo de ver que um raio de luz que atinja o ponto $P_{1}$ ,estando ele se propagando paralelo ao eixo horizontal de coordenadas escolhido, tem uma deflexão de $30$ no sentido horário (para baixo), veja também , que simetricamente, se você escolher um ponto $P'_{1}$ reflexo do ponto original, como sendo o ponto de contato, o raio sofreria uma deflexão de $30$ no sentindo anti horário (para cima). Assim apenas precisamos escolher uma maneira de fazer o ponto $P'_{1}$ ser tal que a reta definida pela direção do raio de luz faça um ângulo de $45$ graus com a normal ao ponto, pois com isso anulamos a deflexão de $30$ graus no sentido horário do primeiro cilindro com uma deflexão igual, e contrária, no sentindo anti horário. Como a reta já faz 30 graus com o eixo horizontal, precisamos apenas que o ponto $P'_{1}$ esteja a $15$ graus do centro de sua circunferência.E não há nenhuma restrição sobre o ponto $P'_{1}$ estar encostado no outro cilindro, então podemos colocar ele em qualquer ponto da nova semirreta gerada pelo prolongamento do raio de luz logo após sair do primeiro cilindro, ou seja, o ponto $P_{1}$ está em qualquer lugar da semirreta que faz $-30$ graus com a horizontal e sai pelo ponto $P_{2}$ . E o centro do outro cilindro está em qualquer lugar da semirreta paralela à antiga, contudo distante da mesma pelo vetor $\vec{r}=R(cos(15^{\circ})\hat{i}+sen(15^{\circ})\hat{j})$ . Ou seja, o lugar geométrico dos nossos centros do cilindro 02, é uma reta.

Problema 3

Podemos aproximar esse processo como sendo isotérmico, dizendo que o mesmo seria muito rápido para variar a energia interna do gás, assim todo trabalho sobre o sistema vira calor pro meio externo, que no caso é o sistema gelo-água:

$Q=W_{ext}=P_{ext} \Delta V$

Basta agora quanta será a variação do volume do gás, isso vem facilmente pela condição de equilíbrio, que é basicamente saber que no final a pressão do gás será igual à pressão externa, pois o pistão deverá estar em equilíbrio, logo, e usando o fato da transformação do gás ser uma isoterma e não há vazão de partículas:

$p_{o} V_{o}=p_{1}V_{1}$

Mas no final temos que $p_{1}=10 atm=10 p_{o}$ , tal que:

$V_{1}=\frac{V_{o}}{10}=0,5 L$

$\Delta V=4,5 L$

$Q=\Delta m L=W_{ext}$

$\Delta m=\frac{p_{ext}\Delta V}{L}$

$\Delta m=\frac{10^6 \cdot 4,5 \cdot 10^{-3}}{33} \approx 136 g$

E vale lembrar que o calor latente de fusão da água veio errado na prova, contudo é ele que devemos usar na solução, pois é o dado da prova.

Obs: Um erro extremamente comum é tomar que o trabalho no gás seria o "trabalho da isoterma", e portanto seria apenas $nRT ln(\frac{V}{V_{o}})$ , mas perceba que isto é o trabalho da isotérmica reversível, que não é tipo de processo estudado nessa questão, visto a espontaneidade do mesmo, então realmente devemos pensar no trabalho a pressão externa constante, que já é conhecido na literatura, para maior embasamento veja "Processos Irreversíveis":

Trabalhos Expansivos (Material da UFRGS)

E argumentos para a espontaneidade, e portanto irreversibilidade, do processo são:

-Abstinência de uma transformação "quase estática"

-Deslocamento do sistema de seu equilíbrio, para entrar em outro equilíbrio, e para chegar de um equilíbrio em outro nós usamos o fato de que a entropia do universo deve ser maximizada, logo existiu aumento de entropia e portanto irreversibilidade, sendo mais formais, podemos dizer que para termos um processo reversível de um estado de equilíbrio A até um estado de equilíbrio B, ele deve ser percorrido por outros estados intermediários que diferem de infinitesimais de estados de equilíbrio, o que não é o caso do problema.

O gás na questão apenas serve para usarmos a equação da isoterma e para termos um mecanismo de transferência de calor pro gelo, que é o surgimento de gradientes de temperatura instantâneos devido ao trabalho externo, mas logo desaparecem com a total transferência de calor para a fusão de gelo, com a temperatura de equilíbrio do sistema inalterada já que todo calor vai pra fusão.

Problema 4

Esse problema é um problema meramente de matemática, onde podemos usar apenas alguns truques simples de combinatória. Pra termos um momento de dipolo de $2 \mu_{o}$ precisamos alinhar 4 partículas para cima e 2 para baixo, pois temos 6. Os dipolos alinhados na mesma direção são indistinguíveis, assim podemos permuta los sem mudar a física da situação. A probabilidade de encontrar o sistema nesse estado é:

$p(4,2)=(\frac{3}{4})^4 (\frac{1}{4})^2 \cdot \dbinom{6}{2}$

Pois temos que escolher 4 pra cima, tendo assim que multiplicar 4 vezes pela probabilidade de ter-lo, também temos que escolher 2 pra baixo, e depois de tudo isso ainda podemos permutar a posição dos pra cima e pra baixo, sendo eles distinguíveis pelo sentido, então temos que multiplicar pelo número de combinações possíveis disso.

$p(4,2)=\frac{1215}{4096} \approx 0,3$

Problema 5

Existem duas abordagens para esse problema, a abordagem com dinâmica e a abordagem com Bernoulli, a abordagem com Bernoulli supõe que o fluxo da água é laminar, o que não é exatamente verdade, e a solução por dinâmica tem lá seus erros, então colocarei as duas soluções desta questão:

1-Bernoulli:

a) Podemos usar, que como o fluxo é laminar e a energia mecânica se conserva:

$p+\rho gh +\frac{\rho v^2}{2}=cte$

Supondo que não há pressão atmosférica, visto que não é dado do problema, temos que:

$\rho gh=\rho \frac{v^2}{2}$

$v=\sqrt{2gh}$

b) Podemos encontrar a força com o impulso, o impulso gerado pela tampa vai ser igual a:

$I=\Delta p=\Delta m v$

$\Delta m=\rho \Delta V$

$\Delta V=a \Delta x=av\Delta t$

$I=F\Delta t=\rho a v^2 \Delta t$

$F=2 \rho gha$

Essa força é justamente o dobro da força do caso em que não há fluxo de água (Pressão hidrostática vezes a área)

2)Dinâmica:

a) O impulso realizado pela pressão hidrostática será:

$I=F\Delta t=\rho g a \Delta t$

E este servirá para acelerar um pedaço de água, que vamos aproximar como indo de 0 até v durante esse processo.

$I=\Delta m v=\rho a v^2 \Delta t=\rho a g \Delta t$

$v=\sqrt{gh}$

b)O método para encontrar a força de reação é exatamente o mesmo da solução anterior, no caso a única coisa que muda é a velocidade do fluxo.

$F=\rho a v^2=\rho gh a$

E esta é a mesma força que haveria se não houvesse o fluxo d'água.

Problema 6

Esse problema tem algumas coisas rápidas de se notar, de primeiro temos, olhando a parte do circuito na chave S1, que o capacitor $C_{1}$ começará com uma diferença de potencial entre 1 e 2 de 6 volts, devido à bateria, sendo o potencial de 2 maior que o de 1, e analogamente para a chave S3, contudo com o potencial 3 maior que o 4. Então, fechando-se a chave começaremos a ter a troca de carga mediada pela "carga", no sentido da engenharia elétrica, que pode ser resistiva ou indutiva. Abrindo em casos:

a) Os capacitores trocarão carga até que estejam com o mesmo potencial, o que quer dizer que no final teremos, usando a lei de Kirchhoff:

Obs: Vamos adotar o sinal de "mais" para a carga positiva do capacitor um e o de menos pra positiva do capacitor dois.

$\sum V_{i}=0$

$\frac{Q_{1}}{C_{1}}-\frac{Q_{2}}{C_{2}}=0$

$Q_{1}=-2 Q_{2}$

E temos também que a soma das cargas dos capacitores se conserva, devido à corrente passando pelos mesmo ser igual:

$Q_{1}-Q_{2}=cte$

No começo:

$Q_{1}=C_{1} V_{o}=120 \mu C$

$Q_{2}=60 \mu C$

$Q_{2,f}=-20 \mu C$

$Q_{1,f}= 40\mu C$

Num tipo de circuito desse, circuito RC de corrente contínua, o sistema chegará no estado estacionário após um certo tempo, pois genericamente temos, para um circuito com capacitor em série com resistor:

$\frac{Q}{C}+RI=0$

Mas podemos relacionar a corrente do sistema com a taxa de variação de carga do capacitor, pois a corrente é a derivada temporal da carga:

$I=\frac{dQ}{dt}$

$\frac{Q}{C}+R \frac{dQ}{dt}$

$\frac{dQ}{Q}=\frac{-dt}{RC}$

E integrando dos dois lados:

$\int_{Q_{o}}^{Q} \frac{dQ}{Q}=-\frac{1}{RC} \int _{0}^{t} dt$

Usando:

$\int_{a}^{b} \frac{dx}{x}=ln(\mid b\mid)-ln(\mid a \mid)$

$ln(\frac{Q}{Q_{o}})=\frac{-t}{RC}$

$Q(t)=Q_{o} e^{\frac{-t}{RC}}$

E soluções para esse tipo de problema, tem, em geral, a mesma taxa de decaimento exponencial. No caso por exemplo de nossos capacitores, eles vão começar no gráfico pelo seus respectivos valores inicias, e serão ligado por uma curva de exponencial com expoente negativo com assíntota na sua carga final, que é o que a carga no infinito deve valer e portanto o valor a qual a carga tem de convergir. Vemos que o circuitos terá um tempo característico que terá valor conseguido com uma simples ideia, como os dois capacitores do problema estão em série, eles se comportarão como um capacitor equivalente de capacitância:

$C_{eq}=\frac{C_{1}C_{2}}{C_{1}+C_{2}}$

$C_{eq}=\frac{20}{3} \mu F$

e assim:

$\tau=RC=2 ms$

Podemos dizer, que a carga de um capacitor será genericamente uma combinação de dois termos, um constante representando a condição de que no começo havia uma carga não nula nele, e outro termo que representa um decaimento ou crescimento exponencial que converge para um resultado, isso se deve à solução que nós encontramos para a carga no item anterior, a corrente ou variação de carga "vê" o circuito com essa capacitância equivalente e interage com ele desta forma, veja bem:

$Q(t)=A+B e^{\frac{-t}{RC}}$

Sendo A e B constantes genéricas que dependem das condições inicias e finais do problema, por exemplo, podemos usar essa equação geral pra Q para encontrar a equação de carga do capacitor 1:

$Q_{1}(\infty)=40=A+B \cdot 0$

$A=40 \mu C$

$Q_{1}(0)=120=40+B \cdot 1$

$B=80 \mu C$

$Q_{1}(t)=40+ 80e^{\frac{-t}{2}}$

Sendo t medido em $ms$ e a carga medida $\mu C$ . E usando as equações análogas pra $Q_{2}$ :

$Q_{2}(t)=-20+80 e^{\frac{-t}{2}}$

E usando a equação $V=\frac{Q}{C}$

$V_{1}(t)=2+4 e^{\frac{-t}{2}}$

$V_{2}(t)=-2+8 e^{\frac{-t}{2}}$

Por efeito de sinal, deixemos as equações na notação da prova, no capacitor 1 devemos ter a diferença de potencial entre a placa 1 e a 2, sendo 1 em geral a de menor potencial,e no começo a placa 3 do capacitor 2 é maior do que a da placa 4, logo:

$V_{1,2}(t)=-2-4 e^{\frac{-t}{2}}$

$V_{3,4}(t)=-2+8 e^{\frac{-t}{2}}$

Ou seja, temos as equações que descrevem nossas voltagens, o gráfico pode ser feito marcando o primeiro ponto e traçando a assíntota da voltagem no infinito, e uma exponencial que converge do primeiro ponto até ela no infinito.

b) Nesse caso nós não teremos uma convergência para uma certa configuração como no sistema anterior, em que há uma dissipação de energia acompanhada de uma falta de periodicidade no sistema. Quando se temos capacitores acoplados a indutores, eles, em geral, tendem a gerar uma função harmônica para tensão e demais propriedades do circuito. Existe um análogo mecânico entre circuitos e sistemas mecânicos, um belo exemplo disso é o circuito $LC$ , o de capacitores e indutores, e seu análogo mecânico é o oscilador massa-mola, que gera uma função harmônica para posição, velocidade e aceleração, já o circuito gerando funções harmônicas para carga, corrente e derivada temporal de corrente.

Obs: Para dar uma explicação mais genérica do fenômeno podemos citar os análogos mecânicos num caso mais geral, um belo exemplo é o circuito do caso "a", temos um resistor e um capacitor, e as propriedades em geral tendendo exponencialmente para um estado de equilíbrio, e isso é análogo a uma partícula se movendo num líquido viscoso, tal que a força de arrasto na mesma é proporcional à sua velocidade. E para um caso mais geral, podemos citar o circuito, por exemplo em série, de um resistor, um capacitor e um indutor, que é análogo a uma partícula presa a uma mola, ocorrendo o movimento do corpo no líquido viscoso citado anteriormente, e o comportamento do sistema pode ser estudado em casos:

-Oscilação Subamortecida: A partícula executará um movimento periódico, contudo, com a amplitude decrescendo exponencialmente ao longo do tempo

-Oscilação Criticamente Amortecida:A partícula exerce um movimento, e para em sua posição de equilíbrio.

-Oscilação Superamortecido:A partícula exerce o movimento e o cessa efetivamente antes de chegar na posição de equilíbrio.

Seguiremos com a mesma abordagem do item anterior, no sentido em que resolveremos o problema a partir da equação gerada pela lei de Kirchhoff, transformando novamente os capacitores num só capacitor equivalente:

$\sum V_{i}=0$

$\frac{Q}{C}+L\frac{dI}{dt}=0$

$\frac{d^2 Q}{dt^2}+\frac{1}{LC} Q=0$

Que é uma equação harmônica, equação de MHS, para a função $Q(t)$ , então devemos ter em geral que:

$Q(t)=A sen(\omega t)+B cos(\omega t)$

sendo $\omega=\sqrt{\frac{1}{LC}}$

$\omega=\frac{1}{4 \cdot 10^{-3}}=250 \frac{rad}{s}$

Devemos então ter que a solução para uma carga $Q_{1}$ ou $Q_{2}$ deve ser analogamente escrita como uma constante mais o termo solução do sistema, que vem da solução do MHS.

$Q_{1}(t)=A+B cos(250 t)+C sen(250 t)$

Com t sendo medido em segundos, e sendo A, B, C constantes genéricas. Sabemos que no começo a corrente no sistema é zero, pois a corrente era zero antes da chave ser fechada e deve continuar instantaneamente pois o indutor impede descontinuidades de corrente, sendo a corrente a derivada temporal da carga, temos que:

$I(t)=250 C cos(250)t -250 B sen(250 t)$

Usando $I(0)=0=250 C$

$C=0$

E isso vale para os dois capacitores, logo:

$Q(t)=A+B cos(250 t)$

Para as duas cargas. No começo, pegando a corrente no sentido horário, vemos que há um ganho de potencial de 12 V percorrendo e consequentemente uma perda de potencial de 12 V no indutor. Logo, usando que:

$I=-\frac{dQ_{1}}{dt}=-\frac{dQ_{2}}{dt}$

Logo:

$L\frac{dI}{dt}=+12 V$

$2,4 (250)^2 B=12$

$B=80 \cdot 10^{-6} C$

$B=80 \mu C$

Usando a condição de que a carga no começo foi a achada em cima:

$Q_{1}(t)=40+80 cos(250 t)$

$Q_{2}(t)=-20+80 cos(250 t)$

Onde as cargas são medidas em $\mu C$ . Ou seja:

$V_{1,2}(t)=-\frac{Q_{1}}{C_{1}}=-2-4 cos(250 t)$

$V_{3,4}=-2+8 cos(250 t)$

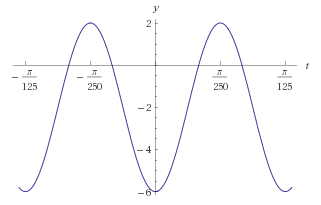
Que resulta em um gráfico de função cosseno com o centro em $(-2)$ nas duas voltagens, sendo a segunda voltagem a de maior amplitude.

Problema 7

Podemos olhar esta reação a partir do centro de momento, em que teremos que a soma dos momentos das partículas resulta no vetor nulo, assim temos que se o sistema for composto de duas partícula, elas terão direção igual e contrária.

Assim, conservando o momento:

$0=m_nv_n+m_av_a$